#> [,1] [,2] [,3] [,4] [,5] [,6] [,7]
#> [1,] 0.23137255 0.1686275 0.19607843 0.2666667 0.3843137 0.4666667 0.5450981
#> [2,] 0.06274510 0.0000000 0.07058824 0.2000000 0.3450980 0.4705882 0.5019608
#> [3,] 0.09803922 0.0627451 0.19215687 0.3254902 0.4313726 0.5058824 0.5098040
#> [4,] 0.12941177 0.1490196 0.34117648 0.4156863 0.4509804 0.4588235 0.4470588
#> [5,] 0.19607843 0.2313726 0.40000001 0.4980392 0.4862745 0.4745098 0.4705882
#> [6,] 0.27843139 0.3294118 0.43137255 0.5058824 0.5333334 0.5137255 0.5058824
#> [7,] 0.38039216 0.4352941 0.48235294 0.5098040 0.5333334 0.5176471 0.4784314
#> [8,] 0.45098040 0.4666667 0.50980395 0.5490196 0.5215687 0.4980392 0.5411765
#> [9,] 0.53725493 0.5019608 0.51764709 0.5019608 0.4666667 0.4823529 0.5019608
#> [10,] 0.60392159 0.6039216 0.61176473 0.5490196 0.4823529 0.4901961 0.4941176
#> [11,] 0.60392159 0.6078432 0.61176473 0.5764706 0.5215687 0.5372549 0.5450981
#> [12,] 0.56862748 0.5725490 0.57254905 0.5294118 0.4980392 0.5058824 0.4588235
#> [13,] 0.55686277 0.5529412 0.54901963 0.5647059 0.5764706 0.4745098 0.3294118
#> [14,] 0.61960787 0.6039216 0.55686277 0.5607843 0.5176471 0.3529412 0.2823530
#> [15,] 0.56862748 0.5843138 0.57647061 0.5764706 0.5333334 0.3137255 0.3490196
#> [16,] 0.58039218 0.5725490 0.56862748 0.5764706 0.5215687 0.2470588 0.2588235
#> [17,] 0.58431375 0.5607843 0.56470591 0.5921569 0.5176471 0.2509804 0.3294118
#> [18,] 0.57647061 0.5254902 0.54901963 0.5803922 0.5294118 0.3921569 0.4235294
#> [19,] 0.59607846 0.4588235 0.44705883 0.4823529 0.4941176 0.4784314 0.3647059
#> [20,] 0.56862748 0.4980392 0.50196081 0.5215687 0.5176471 0.5294118 0.6705883
#> [21,] 0.56078434 0.4980392 0.50588238 0.5058824 0.5098040 0.5490196 0.8588235
#> [22,] 0.56078434 0.4901961 0.51372552 0.5019608 0.4823529 0.6000000 0.5803922
#> [23,] 0.55294120 0.5137255 0.54509807 0.5450981 0.5411765 0.5921569 0.5019608
#> [24,] 0.56078434 0.5450981 0.54117650 0.5843138 0.6274510 0.5882353 0.5764706
#> [25,] 0.58431375 0.5215687 0.53333336 0.5764706 0.5882353 0.6000000 0.6156863
#> [26,] 0.67450982 0.5647059 0.52941179 0.5333334 0.5294118 0.5450981 0.6000000
#> [27,] 0.79215688 0.7333333 0.59215689 0.5019608 0.4784314 0.5254902 0.5568628
#> [28,] 0.84705883 0.7568628 0.65882355 0.5921569 0.5137255 0.4941176 0.5411765
#> [29,] 0.86274511 0.7882353 0.72941178 0.6745098 0.6117647 0.5568628 0.5568628
#> [30,] 0.81568629 0.7882353 0.77647060 0.7490196 0.7176471 0.6705883 0.6235294
#> [31,] 0.70588237 0.6784314 0.72941178 0.7607843 0.7764706 0.7882353 0.7411765
#> [32,] 0.69411767 0.6588235 0.70196080 0.7372549 0.7921569 0.8549020 0.8549020
#> [,8] [,9] [,10] [,11] [,12] [,13] [,14]
#> [1,] 0.5686275 0.5843138 0.5843138 0.5137255 0.4901961 0.5568628 0.5647059
#> [2,] 0.4980392 0.4941176 0.4549020 0.4156863 0.3960784 0.4117647 0.4431373
#> [3,] 0.4745098 0.4431373 0.4392157 0.4392157 0.4156863 0.4117647 0.5019608
#> [4,] 0.4117647 0.4196078 0.4745098 0.4901961 0.4274510 0.4431373 0.5725490
#> [5,] 0.4470588 0.4196078 0.4901961 0.5058824 0.4156863 0.4235294 0.4862745
#> [6,] 0.4666667 0.4235294 0.4784314 0.4823529 0.4117647 0.4196078 0.4352941
#> [7,] 0.4745098 0.4980392 0.5411765 0.4862745 0.4705882 0.4196078 0.3137255
#> [8,] 0.5372549 0.5137255 0.5215687 0.5254902 0.4235294 0.2823530 0.2000000
#> [9,] 0.5098040 0.4745098 0.5372549 0.5137255 0.2901961 0.2117647 0.1960784
#> [10,] 0.4980392 0.5215687 0.5176471 0.3529412 0.2470588 0.2431373 0.2745098
#> [11,] 0.5254902 0.5529412 0.4745098 0.3137255 0.3803922 0.3529412 0.3843137
#> [12,] 0.4039216 0.5098040 0.4705882 0.4352941 0.5725490 0.5333334 0.6392157
#> [13,] 0.3450980 0.4274510 0.3960784 0.5411765 0.8352941 0.6980392 0.7490196
#> [14,] 0.3176471 0.3294118 0.4196078 0.6470588 0.8980392 0.7176471 0.7490196
#> [15,] 0.4117647 0.3764706 0.5058824 0.7529412 0.7254902 0.5686275 0.7960784
#> [16,] 0.3450980 0.4431373 0.7137255 0.8627451 0.5411765 0.6352941 0.8078431
#> [17,] 0.4392157 0.6392157 0.8745098 0.8078431 0.5686275 0.7686275 0.8000000
#> [18,] 0.5647059 0.8235294 0.9725490 0.6862745 0.6862745 0.8627451 0.8862745
#> [19,] 0.7019608 0.9333333 0.9725490 0.6666667 0.7254902 0.9450980 0.9019608
#> [20,] 0.9294118 0.9882353 0.8980392 0.6784314 0.6627451 0.8627451 0.7607843
#> [21,] 0.9568627 0.8235294 0.7568628 0.6509804 0.6000000 0.7490196 0.7019608
#> [22,] 0.6509804 0.7372549 0.7137255 0.6705883 0.6470588 0.7647059 0.7450981
#> [23,] 0.5333334 0.6862745 0.6784314 0.7411765 0.8039216 0.7882353 0.6588235
#> [24,] 0.5921569 0.6627451 0.6549020 0.7019608 0.8313726 0.7960784 0.8117647
#> [25,] 0.6352941 0.6862745 0.7450981 0.6509804 0.7921569 0.8784314 0.7725490
#> [26,] 0.6392157 0.6509804 0.7215686 0.6509804 0.5882353 0.7215686 0.6117647
#> [27,] 0.5882353 0.6000000 0.5803922 0.5294118 0.4980392 0.6000000 0.6509804
#> [28,] 0.5647059 0.5568628 0.5372549 0.4705882 0.5137255 0.5686275 0.5647059
#> [29,] 0.6000000 0.5882353 0.5450981 0.4941176 0.5333334 0.5803922 0.5529412
#> [30,] 0.5764706 0.5294118 0.5098040 0.5450981 0.5764706 0.5647059 0.5686275
#> [31,] 0.6784314 0.6117647 0.5450981 0.5568628 0.5686275 0.5529412 0.5529412
#> [32,] 0.8117647 0.7490196 0.6862745 0.6509804 0.6392157 0.6392157 0.6313726
#> [,15] [,16] [,17] [,18] [,19] [,20] [,21]
#> [1,] 0.5372549 0.5058824 0.5372549 0.5254902 0.4862745 0.5450981 0.5450981
#> [2,] 0.4274510 0.4392157 0.4666667 0.4274510 0.4117647 0.4901961 0.4980392
#> [3,] 0.4862745 0.5098040 0.4980392 0.4784314 0.4509804 0.4705882 0.5098040
#> [4,] 0.5215687 0.4980392 0.4627451 0.4588235 0.4980392 0.4784314 0.5176471
#> [5,] 0.4745098 0.4235294 0.3843137 0.4313726 0.4588235 0.4705882 0.5254902
#> [6,] 0.4235294 0.3843137 0.3686275 0.3803922 0.3254902 0.3450980 0.4000000
#> [7,] 0.2666667 0.2901961 0.3960784 0.4117647 0.2549020 0.2274510 0.2470588
#> [8,] 0.1607843 0.2823530 0.7098039 0.8196079 0.4901961 0.2666667 0.2509804
#> [9,] 0.1725490 0.3372549 0.7960784 0.8509804 0.6352941 0.3921569 0.3019608
#> [10,] 0.3098039 0.4039216 0.5960785 0.5803922 0.5529412 0.4745098 0.3960784
#> [11,] 0.5372549 0.5450981 0.5803922 0.5254902 0.5411765 0.5254902 0.5490196
#> [12,] 0.6627451 0.5960785 0.6313726 0.5803922 0.6941177 0.6313726 0.7647059
#> [13,] 0.8274510 0.7411765 0.8039216 0.8117647 0.8352941 0.7490196 0.7803922
#> [14,] 0.9372549 0.8588235 0.8941177 0.8823529 0.8392157 0.8470588 0.8235294
#> [15,] 0.8745098 0.9490196 0.9568627 0.9333333 0.9450980 0.8901961 0.8823529
#> [16,] 0.7686275 0.9686275 1.0000000 1.0000000 0.9607843 0.9254902 0.9019608
#> [17,] 0.8627451 0.9529412 0.9607843 0.9372549 0.9176471 0.9058824 0.7647059
#> [18,] 0.9019608 0.9137255 0.8784314 0.7882353 0.7215686 0.7098039 0.7450981
#> [19,] 0.7333333 0.7058824 0.6509804 0.5725490 0.5843138 0.6156863 0.7215686
#> [20,] 0.4823529 0.5294118 0.4980392 0.5921569 0.6470588 0.5176471 0.5921569
#> [21,] 0.5019608 0.5764706 0.5843138 0.6745098 0.5764706 0.5019608 0.5529412
#> [22,] 0.5960785 0.5607843 0.5960785 0.6000000 0.5568628 0.5529412 0.5294118
#> [23,] 0.5921569 0.5686275 0.5725490 0.5843138 0.6000000 0.5843138 0.5647059
#> [24,] 0.5843138 0.5450981 0.5647059 0.5372549 0.5921569 0.6078432 0.5960785
#> [25,] 0.7529412 0.7058824 0.5725490 0.4941176 0.5529412 0.6117647 0.6000000
#> [26,] 0.6196079 0.6588235 0.5843138 0.5294118 0.5098040 0.5176471 0.5019608
#> [27,] 0.5607843 0.5098040 0.5019608 0.5921569 0.5960785 0.5294118 0.5450981
#> [28,] 0.5372549 0.4980392 0.4941176 0.5450981 0.6000000 0.5843138 0.5490196
#> [29,] 0.5137255 0.4941176 0.4980392 0.5411765 0.5882353 0.6039216 0.5843138
#> [30,] 0.5372549 0.5333334 0.5372549 0.5803922 0.5960785 0.5882353 0.6078432
#> [31,] 0.5450981 0.5490196 0.5607843 0.5450981 0.5411765 0.5607843 0.5725490
#> [32,] 0.6000000 0.6235294 0.6352941 0.5843138 0.5490196 0.5803922 0.6313726
#> [,22] [,23] [,24] [,25] [,26] [,27] [,28]
#> [1,] 0.5215687 0.5333334 0.5450981 0.5960785 0.6392157 0.6588235 0.6235294
#> [2,] 0.4784314 0.5137255 0.4862745 0.4745098 0.5137255 0.5176471 0.5215687
#> [3,] 0.5137255 0.5450981 0.4980392 0.4941176 0.4980392 0.5098040 0.5568628
#> [4,] 0.5372549 0.5333334 0.5137255 0.4862745 0.5098040 0.5176471 0.5294118
#> [5,] 0.5490196 0.5137255 0.5529412 0.5294118 0.4980392 0.4745098 0.4666667
#> [6,] 0.3803922 0.3450980 0.4627451 0.5490196 0.5333334 0.4705882 0.4196078
#> [7,] 0.3058824 0.5333334 0.4784314 0.5450981 0.5921569 0.5058824 0.4235294
#> [8,] 0.3215686 0.4823529 0.4392157 0.5294118 0.5921569 0.5372549 0.4470588
#> [9,] 0.2941177 0.2901961 0.2980392 0.4196078 0.5294118 0.5294118 0.5058824
#> [10,] 0.3764706 0.3372549 0.2941177 0.3960784 0.5333334 0.5333334 0.5254902
#> [11,] 0.6862745 0.5568628 0.4000000 0.4235294 0.5294118 0.5137255 0.5215687
#> [12,] 0.8196079 0.7411765 0.4901961 0.4235294 0.5490196 0.5372549 0.5176471
#> [13,] 0.7372549 0.6313726 0.5098040 0.4862745 0.5137255 0.5098040 0.5137255
#> [14,] 0.7843137 0.7411765 0.6823530 0.6313726 0.5450981 0.5254902 0.4941176
#> [15,] 0.9215686 0.8588235 0.8784314 0.8431373 0.6117647 0.5019608 0.5058824
#> [16,] 0.8431373 0.9058824 0.9803922 0.9450980 0.6196079 0.4901961 0.4941176
#> [17,] 0.5882353 0.8156863 0.9803922 0.8901961 0.6392157 0.5686275 0.5607843
#> [18,] 0.6666667 0.7019608 0.9058824 0.8745098 0.6352941 0.5725490 0.5490196
#> [19,] 0.8470588 0.8313726 0.9254902 0.9254902 0.6509804 0.5333334 0.5254902
#> [20,] 0.7921569 0.9411765 0.9411765 0.8705882 0.6117647 0.4666667 0.4705882
#> [21,] 0.6784314 0.7921569 0.7450981 0.7764706 0.5960785 0.3921569 0.4274510
#> [22,] 0.5333334 0.5803922 0.5529412 0.5529412 0.5411765 0.4352941 0.4352941
#> [23,] 0.5647059 0.5686275 0.5607843 0.5058824 0.4823529 0.4862745 0.4431373
#> [24,] 0.5490196 0.4196078 0.3568628 0.3294118 0.4117647 0.5176471 0.4627451
#> [25,] 0.4509804 0.3019608 0.3098039 0.3647059 0.4941176 0.5215687 0.4666667
#> [26,] 0.4980392 0.5294118 0.5607843 0.5450981 0.5333334 0.4980392 0.4745098
#> [27,] 0.6078432 0.6313726 0.6039216 0.6039216 0.5607843 0.5098040 0.5176471
#> [28,] 0.5294118 0.5764706 0.5803922 0.5843138 0.5843138 0.5372549 0.5607843
#> [29,] 0.4862745 0.4941176 0.5529412 0.5686275 0.5764706 0.4980392 0.4470588
#> [30,] 0.5411765 0.4705882 0.5019608 0.5568628 0.5294118 0.3529412 0.1960784
#> [31,] 0.5294118 0.4588235 0.4392157 0.4784314 0.4078431 0.2274510 0.1333333
#> [32,] 0.5647059 0.4392157 0.4666667 0.5098040 0.4705882 0.3607843 0.4039216
#> [,29] [,30] [,31] [,32]
#> [1,] 0.6196079 0.6196079 0.5960785 0.5803922
#> [2,] 0.5215687 0.4823529 0.4666667 0.4784314
#> [3,] 0.5098040 0.4627451 0.4705882 0.4274510
#> [4,] 0.5098040 0.4901961 0.4745098 0.3686275
#> [5,] 0.4039216 0.3411765 0.2941177 0.2627451
#> [6,] 0.3450980 0.2627451 0.1372549 0.1254902
#> [7,] 0.3725490 0.3764706 0.3490196 0.2588235
#> [8,] 0.4117647 0.3960784 0.4941176 0.4000000
#> [9,] 0.4980392 0.4666667 0.4901961 0.5254902
#> [10,] 0.5215687 0.5176471 0.5019608 0.5215687
#> [11,] 0.5411765 0.5333334 0.5098040 0.5254902
#> [12,] 0.5333334 0.5215687 0.5176471 0.5215687
#> [13,] 0.5254902 0.5294118 0.5333334 0.5215687
#> [14,] 0.5137255 0.5568628 0.5333334 0.5411765
#> [15,] 0.5137255 0.5215687 0.5019608 0.5098040
#> [16,] 0.4862745 0.4901961 0.4941176 0.4862745
#> [17,] 0.5490196 0.5333334 0.4745098 0.4470588
#> [18,] 0.5450981 0.5686275 0.5568628 0.5019608
#> [19,] 0.5098040 0.4980392 0.5372549 0.5921569
#> [20,] 0.4392157 0.3921569 0.3882353 0.5490196
#> [21,] 0.4666667 0.4745098 0.4235294 0.5333334
#> [22,] 0.4745098 0.5058824 0.5411765 0.7019608
#> [23,] 0.4235294 0.4431373 0.5803922 0.7803922
#> [24,] 0.3764706 0.4000000 0.6235294 0.7450981
#> [25,] 0.4431373 0.5490196 0.7333333 0.6039216
#> [26,] 0.5294118 0.7411765 0.8274510 0.5333334
#> [27,] 0.6705883 0.8431373 0.7294118 0.4588235
#> [28,] 0.7960784 0.8078431 0.4862745 0.2784314
#> [29,] 0.7294118 0.6784314 0.2196078 0.1294118
#> [30,] 0.5372549 0.6274510 0.2196078 0.2078431
#> [31,] 0.5137255 0.7215686 0.3803922 0.3254902
#> [32,] 0.6666667 0.8470588 0.5921569 0.4823529Convolutional
Neural Networks
Model Building
R Packages
Python Data
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
batch_size = 4
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')Building CNNs
Building CNNs
Input Data
Convolutional Block
CNN Architecture
R CIFAR
Input Data
Building CNNs
Input Data
Convolutional Block
CNN Architecture
R CIFAR
Input Data

Channels

Data - Red
Convolutional Block
Building CNNs
Input Data
Convolutional Block
CNN Architecture
R CIFAR
Convolutional Block
A convolutional block (layer) is the process where a matrix (array) of data undergoes the following process.
- Apply a convolutional filter
- Fold the channels
- Pool the data
Convolution Filter
A Convolution Filter will highlight certain features of an image.
The matching features will contain a large value.
Dismatching features will contain a smaller value.
Convolution Filter
\[ \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \\ j & k & l \end{array} \right) \]
\[ \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \]
\[ \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \\ j & k & l \end{array} \right) * \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \]
\[ \left( \begin{array}{cc} a\alpha + b\beta + d\gamma + w\delta & b\alpha + c\beta + e\gamma + f\delta \\ d\alpha + e\beta + g\gamma + h\delta & e\alpha + f\beta + h\gamma + i\delta \\ g\alpha + h\beta + j\gamma + k\delta & h\alpha + i\beta + k\gamma + l\delta \end{array} \right) \]
Data Example
\[ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) * \left( \begin{array}{cc} 1/2 & 1/3 \\ 1/3 & 1/2 \end{array} \right) \]
\[ \left( \begin{array}{cc} 1/2 + 2/3 + 4/3 + 5/2 & 1 + 1 + 5/3 + 3 \\ 2 + 5/3 + 7/3 + 4 & 5/2 + 2 + 8/3 + 9/2 \end{array} \right) \]
Folding
Folding is the process when we combine channels together. It is common to add the channels together once the convolution filter is applied to each one.
Folding Example
\[ \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) + \left( \begin{array}{cc} 5 & 6 \\ 7 & 8 \end{array} \right) + \left( \begin{array}{cc} 9 & 10 \\ 11 & 12 \end{array} \right) \]
\[ \left( \begin{array}{cc} 15 & 18 \\ 21 & 24 \end{array} \right) \]
Pooling Layers
The act of summarizing a large matrix to a smaller matrix.
Max Pool
\[ \left[ \begin{array}{cccc} 1 & 3 & 9 & 5 \\ 6 & 2 & 3 & 4 \\ 1 & 0 & 6 & 4 \\ 8 & 4 & 2 & 7 \end{array} \right] \rightarrow \left[ \begin{array}{cc} 6 & 9 \\ 8 & 7 \end{array} \right] \]
Overall
\[ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) \]
\[ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) \]
\[ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) \]
\[ \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) * \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \]
\[ \left( \begin{array}{ccc} 10 & 20 & 30 \\ 40 & 50 & 60 \\ 70 & 80 & 90 \end{array} \right) * \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \]
\[ \left( \begin{array}{ccc} 100 & 200 & 300 \\ 400 & 500 & 600 \\ 700 & 800 & 900 \end{array} \right) * \left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right) \]
\[ \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) + \left( \begin{array}{cc} 5 & 6 \\ 7 & 8 \end{array} \right) + \left( \begin{array}{cc} 9 & 10 \\ 11 & 12 \end{array} \right) \]
\[ \left( \begin{array}{cc} 15 & 18 \\ 21 & 24 \end{array} \right) \]
\[ \left[ \begin{array}{cccc} 1 & 3 & 9 & 5 \\ 6 & 2 & 3 & 4 \\ 1 & 0 & 6 & 4 \\ 8 & 4 & 2 & 7 \end{array} \right] \rightarrow \left[ \begin{array}{cc} 6 & 9 \\ 8 & 7 \end{array} \right] \]
CNN Architecture
Building CNNs
Input Data
Convolutional Block
CNN Architecture
R CIFAR
CNN Architecture

Convolutional Block 1
- Given an 3 channels (3 matrix)
- Apply a \(k_1 \times k_1\) convolutional filter for each individual channel
- Add up the results for each channel by convolutional filter
- Apply a activation function
- Pool the data using a \(\varrho_1 \times \varrho_1\) window matrix
- Repeat the process for the remaining \(\varkappa_1\) filters
- The number of channels available as input
- The size of the convolutional filter (\(k_1\))
- The activation function
- The pooling mechanism
- Define the size of the window matrix (\(\varrho_h\))
- Define how many convolutional filters will be used (\(\varkappa_1\))
Convolutional Block 2 (h=2)
- Use the number of channels from the previous block (\(\varkappa_1\))
- Apply a \(k_2 \times k_2\) convolutional filter for each individual channel
- Add up the results for each channel by convolutional filter
- Apply a activation function
- Pool the data using a \(\varrho_2 \times \varrho_2\) window matrix
- Repeat the process for the remaining \(\varkappa_2\) filters
- The number of channels available as input
- The size of the convolutional filter (\(k_2\))
- The activation function
- The pooling mechanism
- Define the size of the window matrix (\(\varrho_h\))
- Define how many convolutional filters will be used (\(\varkappa_2\))
Convolutional Block 2+ (h=h)
- Use the number of channels from the previous block (\(\varkappa_{h-1}\))
- Apply a \(k_h \times k_h\) convolutional filter for each individual channel
- Add up the results for each channel by convolutional filter
- Apply a activation function
- Pool the data using a \(\varrho_h \times \varrho_h\) window matrix
- Repeat the process for the remaining \(\varkappa_h\) filters
- The number of channels available as input
- The size of the convolutional filter (\(k_h\))
- The activation function
- The pooling mechanism
- Define the size of the window matrix (\(\varrho_h\))
- Define how many convolutional filters will be used (\(\varkappa_h\))
Flattening
Once the images has been pooled to a select pixels or features. The images are flattened to a set of inputs.
These inputs are used to a traditional neural network to classify an image.
Hidden Layers
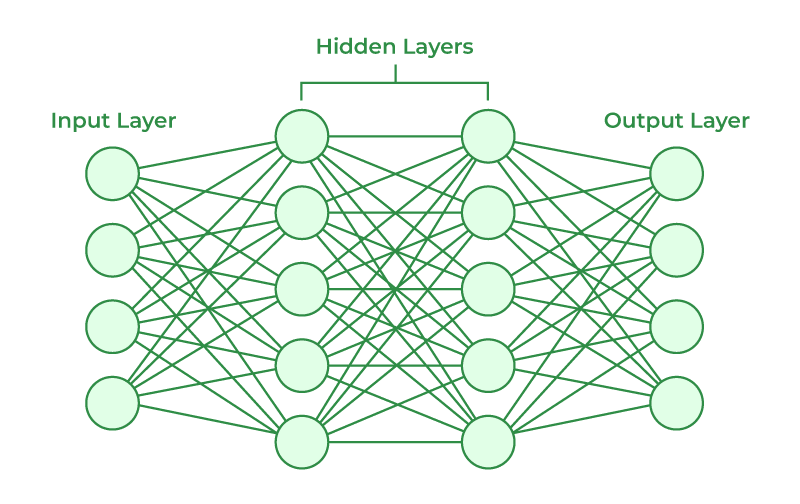
Neural Network

Loss Function
Mean Squared Error
\[ \frac{1}{n}\sum^n_{i-1}\left\{Y_i-f(\boldsymbol X; \boldsymbol \theta)\right\}^2 \]
Cross-Entropy
\[ - \sum^n_{i=1}\sum^k_{j=1} Y_{ij}\log\left\{f_j(\bX_i;\btheta)\right\} \]
\(\btheta\) represents all the parameters in the convolutional filters and hidden layers.
Training
The CNN is trained by supplying a set of pre-classified images.
The parameters in the convolution filters and are estimated using standard techniques:
- Stochastic Gradient Descent
R CIFAR
Building CNNs
Input Data
Convolutional Block
CNN Architecture
R CIFAR
Process
- Load R Packages
- Load Data
- Define Convolutional Block
- Define Model
- Train Model
CIFAR-10 Data
The Canadian Institute for Advanced Research (CIFAR) provides a collection of 60,000 images that are classified in 10 categories. Each image has 32 by 32 pixels.
CIFAR-10 Classes
- airplanes
- cars
- birds
- cats
- deer
- dogs
- frogs
- horses
- ships
- trucks
CIFAR-10 Example

Torch Packages in R
CIFAR-10 Data
- Define Directory
- You may need to change it
- Try this
"."
- Load training CIFAR-10 Data
- Load testing CIFAR-10 Data
- Create Data Loader
- Will create batches of data (128 images)
- Load each batch one at a time instead of the entire thing.
Convolutional Block
- Define Convolutional Block
- Indicate Kernel Filter Size
- \(3\times 3\) Matrix
- Fold by adding
- Apply Rectified Linear Unit
- Pool Matrix
- Max Function
- Window: \(3\times 3\) Matrix
- Indicate Kernel Filter Size
conv_block <- nn_module(
initialize = function(in_channels, out_channels) {
self$conv <- nn_conv2d(
in_channels = in_channels,
out_channels = out_channels,
kernel_size = c(3,3),
padding = "same"
)
self$relu <- nn_relu()
self$pool <- nn_max_pool2d(kernel_size = c(2,2))
},
forward = function(x) {
x |>
self$conv() |>
self$relu() |>
self$pool()
}
)Model
- Using the defined convolutional block
- First Block
- 3 channels; 8 kernel filters
- Second Block
- 8 channels; 16 kernel filters
- First Block
- Flatten matrices (1024 paremeters)
- Apply Neural Network
- 50% dropout
- Linear Model
- Rectified Linear Unit
- Output layer: 10 functions
model <- nn_module(
initialize = function() {
self$conv <- nn_sequential(
conv_block(3, 8),
conv_block(8, 16)
)
self$output <- nn_sequential(
nn_dropout(0.5),
nn_linear(1024, 16),
nn_relu(),
nn_linear(16, 10)
)
},
forward = function(x) {
x |>
self$conv() |>
torch_flatten(start_dim = 2) |>
self$output()
}
)Fitting Model
- Setup
- Loss Function (Cross-Entropy)
- Optimizer
- Metrics
- Learning Rate
- Train the Model
- Define Training Data
- Number of Epochs
- This may take +5 minutes
- Discuss with your table the convolutional block
- Comment the code.
Plot Loss
m408.inqs.info/lectures/7a